Main Index Page

Last updated 20/9/2025

x

The work is a guide to the use of a series of very simple paperfolds intended to be used to teach geometrical ideas in the elementary class (ie the two years above kindergarten).

The work extends the range of Froebel's original Folds of Knowledge by showing how the square can be folded into other geometrical shapes, in particular using folds of 22.5, 30, and 60 degrees.

A full copy of the work can be accessed online here.

**********

***********

The Foreword sets out Koehler's belief that Froebel's methodology is applicable not only to the kindergarten (for children aged 3 to 6) but also in elementary school (children aged 6 to 9).

**********

The Introduction is mainly a long discussion of pedagogy without specific reference to paperfolding, but on page 15 he says, roughly translated, 'Based on the truth that one achieves more with students by having them work on a few objects thoroughly rather than hundreds of them superficially ... I propose the (use of the) Froebel leaflet for the first two school years. It is particularly suitable for giving students a thorough visualisation and understanding of some of the elementary geometric shapes. It is a square cut out of paper, approximately one twentieth the size of an ordinary sheet' and goes on on page 16 to set out the advantages he feels creating geometrical forms by paperfolding has over copying them from a blackboard.

**********

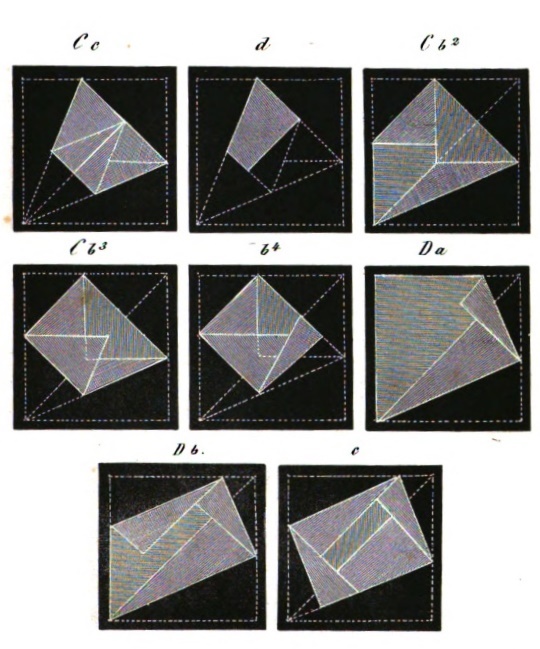
Analysis

The forms illustrated in this analysis are not shown in the order in which they appear in the work.

**********

Forms created using 90 / 45 degree golding geometry

The main sequence begins with the unfolded square and ends with the Double Blintz Basic Form (32 picture d below), at which point the author comments, roughly translated, 'We finally get the basic form, the fourth part of the whole, from which one can learn the most varied forms of life and beauty with constant application of the law of opposites.' No examples of such forms are given in the book but the footnote referring to this sentence says, roughly, 'In a subsequent booklet the leaflet (ie Frobel's use of the folded square) will be revised in its entirety for kindergarten use. This also includes the new folding briefly mentioned in issue 8 of our monthly magazine 'Kindergarten and Elementerklasse' 1861' Weimar, H Bohlau' and adds 'For this purpose Miss D Breymann in Wayum has kindly made her well-thought-out course on the forms of beauty available to me.'

The author then adds:

'By insisting on a precise and beautiful execution of the forms the students will achieve great dexterity, their sense of order and beauty will be trained, and thus another not unimportant benefit for practical life will be gained.'

And:

'Paper folded in ths way could also be used for drawing, colouring and cutting out after such exercises as the following figures show.'

**********

The next page shows other forms which can be created using 90 / 45 degree folding geometry. There is no explanatory text for these illustrations

**********

Forms created using 90/45/22.5 degree folding geometry

The next few pages explain this folding sequence which is based on folding edges onto a diagonal.

**********

**********

**********

Page 38 explains how a crease patterns created using 22.5 degree creases can also be used for tracing, colouring and cutting out. The second paragraph says, roughly, 'As the following examples show, the shapes can also be arranged one below the other. By using the above course of studsy, the child receives the same material that Froebel presented under the name 'Legetafelchen' (laying boards)'.

**********

Forms created using 30/60/120 degree folding geometry

A second sequence of folds shows how to create angles of 60 degrees and how to produce a 60/120 rhombus and an equilateral triangle.

**********