| The Public Paperfolding History Project
Last updated 23/1/2024 x |
|||||||
| At Home Tonight by Herbert McKay, 1940 | |||||||
| 'At
Home Tonight' by Herbert McKay was published by Oxford
University Press in London, New York and Toronto in 1940.
It contains a chapter on Paper-Folding, another on Simple
Home Craftwork which also contains some items involving
folding paper, as does a chapter on Parlour Science.
There is also an interesting chapter on Geometry by
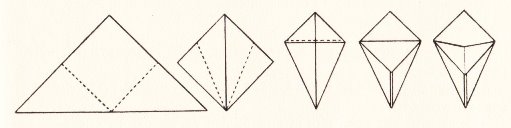
Paper-Folding. There is no general introduction but in his very brief introduction to the Paper-Folding chapter the author states 'Some of the models described here are traditional but there are many variants and new additions', presumably, the work of the author himself. This idea is reinforced by a comment at the start of the instructions for 'A Boat with a Sail' where the author says 'Now let us see what we can do to add details to the paper boat, just as we added them to the cocked hat.' The author also states 'Except in making the original square there is no cutting or tearing', which seems a carry over from the Froebelian tradition, those paperfolding items which do make use of cutting or tearing being explained in the Simple Home Craftwork chapter (except for An Ornamental Cover, which seems to have been displaced from the Craftwork chapter in order to fill space at the end of the Paper-Folding chapter). I have not included all the items in the Craftwork chapter below. The relevant contents are: Paper-Folding Note that the various Ornaments in this chapter are not either numbered or given individual names in the original. They simply follow each other within the 'Ornaments' section. ********** A Cocked Hat - The Pyramidal Hat (but folded from a square)
********** A Sou'wester - The Sou'wester
********** A Dustman's Hat
********** A Hat with Wings (from the preliminary fold)
********** An Ornamental Hat
********** A Hat with a Feather
********** A Military Hat (From the waterbomb base)
********** A Grenadier's Hat
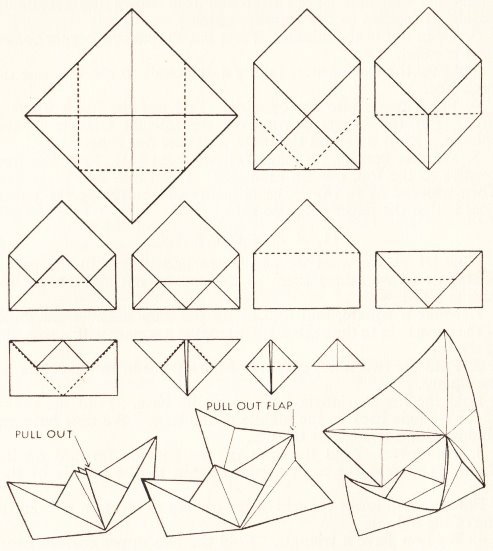
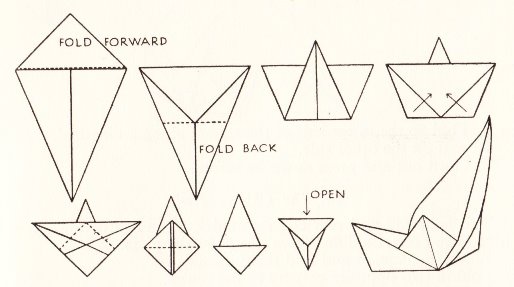
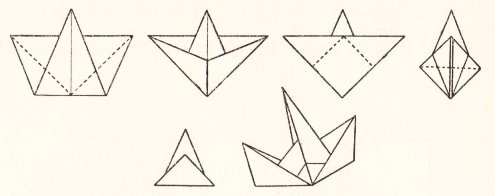
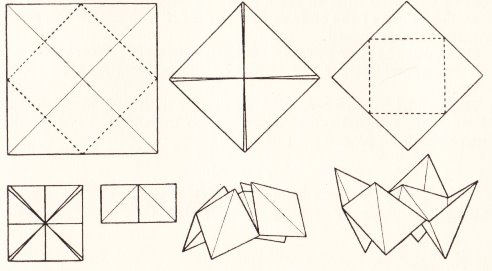
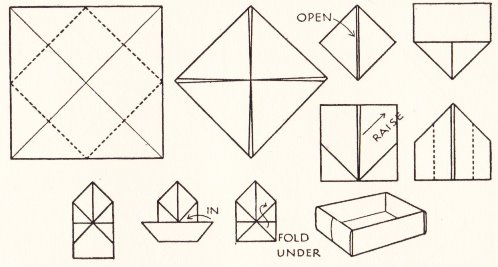
********** A Ship - The Paper Boat (but folded from a square)
********** A Boat with a Sail
********** A Triangular Sail
********** A Ship with a Mast
********** The Chinese Junk
********** A Barge (A variation of the Chinese Junk - still folded from a square - which produces a longer boat)
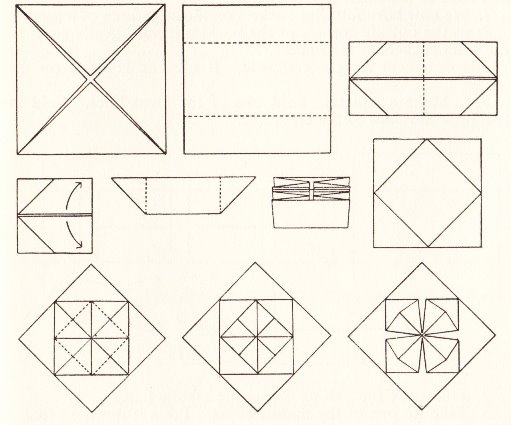
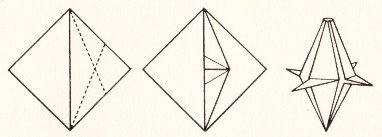
********** Ornament 1 (From the waterbomb base)
********** Ornament 2 (From the waterbomb base. Note that this ornament has a flat base on which it will stand)
********** Ornament 3 (from the preliminary fold)
********** Ornament 4
********** Ornament 5
********** Ornament 6
********** A Tidy (This design is intended to be fixed to a wall with a drawing pin)
********** A Cruet, or Sweetholder - The Salt Cellar
********** A Kettle - The Kettle
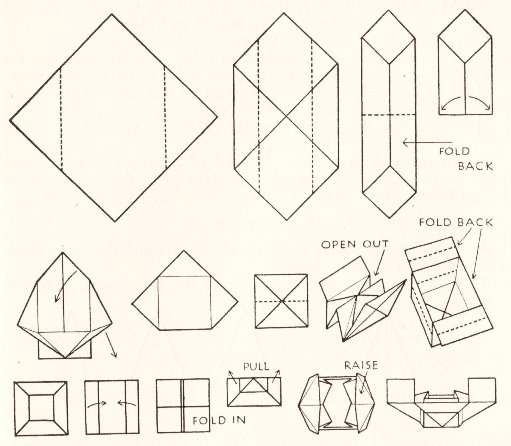
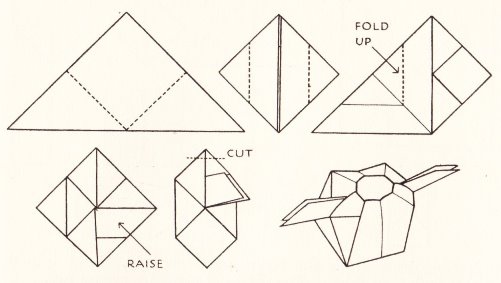
********** Dermot's Box The author comments that 'This is, I think, the strongest and best of the boxes that can be made by paper-folding.' The author does not say why the box was given this particular name.
********** Bellows - The Bellows
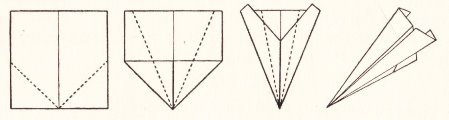
********** A Glider - The Paper Dart (From a square)
********** An Ornamental Cover
********** Simple Home Craftwork ********** A Cracker - A Paper Pop Gun
********** A Note-Case - The Chinese Wallet
********** The Dancers (This is similar to 'Guests' in Margaret Campbell's 'Paper Toy Making' except that in this case the circle of figures is intended to stand upright rather than lay flat)
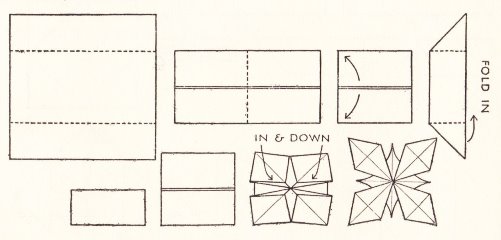
********** Spinners - The Cut and Fold Windmill
********** Puff Ball - The Slit and Assemble Sphere
********** Paper Mats - The Paper Doily
********** Parlour Science ********** Unnamed in the text - The Propellor
********** 'A very elegant glider'
********** Geometry by Paper-Folding Not all the items in this chapter are included here. I am happy to supply further details to anyone who would like them. ********** Division into Thirds (by comparison by eye that two lengths are equal)
********** Making a Right Angle (from an irregularly shaped sheet of paper)
********** Making an Oblong (from an irregularly shaped sheet of paper)
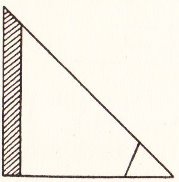
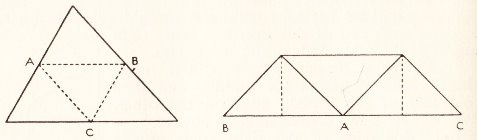
********** The Angles of a Triangle - Summing the Angles of a Triangle (demonstrating, by folding, that the angles of a triangle sum to 180 degrees)
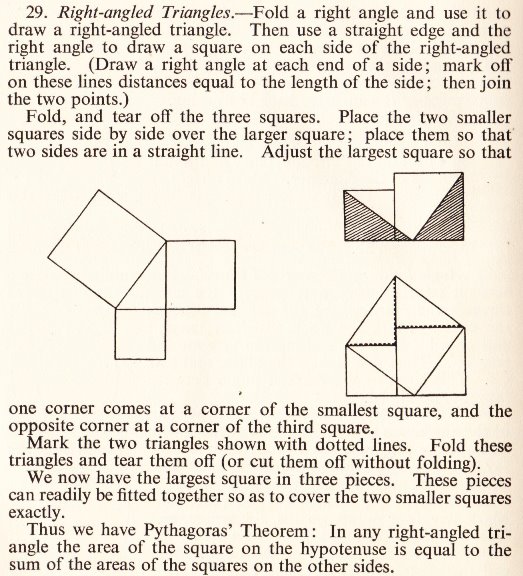
********** Pythagorus' Theorem (demonstrating that the theorem is true by folding and tearing)
********** |
|||||||